夏树的C语言篇 – 简易Kmeans类聚算法实现对点集的分组

0.写在前面

夏树大一上学期为时一周的C语言课设就在昨天周五结束了。其中印象比较深刻的就是课设中有一题运用Kmeans算法对点集实现分组的题目啦(顺便自己试着摸了下GDI的一些函数)，然后今天抽出些时间来整理一下，先上最后实现的结果：

kmeans-best-grouping_1.jpg

kmeans-best-grouping_2.jpg

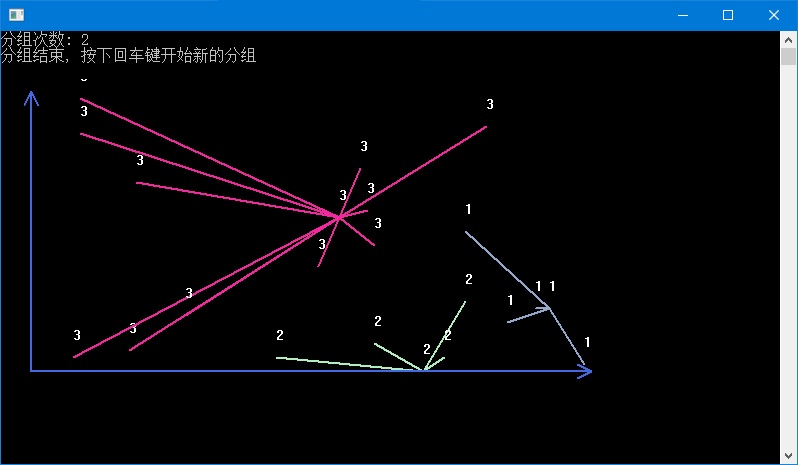
1.问题描述

随机生成一组位于二维坐标系的点集（15<=点集元素个数N<=65），这些点不重合，每个点的位置由x,y值决定，x,y为整数且0<x<80,0<y<40。现在想知道这些点按距离远近该分成几个组合适，已知分组值K备选范围从1-10，输入K值，请你按以下方法画出分组结果：

  • (1) 从N个数据点中随机挑选K个不同点作为K个组的初始中心起点（组中心）；
  • (2) 计算所有点到K个组中心的距离（欧式距离），并把它归到距离最近的组（如果有多个组距离一样，随便选一个归入）；
  • (3) 更新K个组的中心值（求出该组所有点的x平均值和y平均值，作为新的组中心）；
  • (4) 重复（2）~（3）步直至新的组中心和原来的组中心差值小于指定阈值（人为设置），或超出最大重复次数（人为设置），算法结束；
  • (5) 在控制台画出K组分组结果，每组用不同数字表示，使用0,1,2,3….9分别表示10个组。

2.解决思路

2.1.随机生成不重复的二维坐标点集

首先根据题目的意思，生成15-65个点组成二维坐标系的点集(这里有自定义了一个查询重复点坐标的函数int isRandCoordRepeat(int x,int y,COORD coord[],int n);)：

/*初始化随机坐标数组*/
/*返回生成的坐标数量*/
int initRandCoord(COORD coord[], int minN, int maxN)
{
	int x,y;
	int cnt=0,i,n;
	srand((unsigned)time(0));
	n = rand()%(maxN+1)+minN;
	srand((unsigned)time(0));
	for(i=0;i<n;i++)
	{
		x = rand()%80+1;
		y = rand()%40+1;
		while(isRandCoordRepeat(x,y,coord,cnt))
		{
			x = rand()%80+1;
			y = rand()%40+1;
		}
		coord[i].X = x;
		coord[i].Y = y;
		cnt++;
		if(cnt>=maxN)
		{
			break;
		}
	}
	return cnt;
}

2.2初始化k个中心点

这边定义了一个结构体CENTER用来存储中心点变量的一些结构类型, 但是存储点集分组情况的变量g_group和存储点集坐标的变量g_coord是分开的(做到后面有点点懒，就没有再新定义结构体了，不然有点上头)

struct CENTER{
	int X;
	int Y;
	int tryCnt;  //之后用来存储微调中心点的重复次数
	int flag;    //单个点能否继续微调的标志
	int color;   //GDI绘制该分组情况的颜色
}

由用户输入k值，从刚刚生成的点集中挑选k个作为最初的中心点

/*初始化中心点*/
void initCenterDot(COORD coord[], int cnt, struct CENTER center[], int k)
{
	int i,rndNum,x,y;
	COORD centerTmp[10];
	srand((unsigned)time(0));
	/*无重复初始化中心点*/
	for(i=0;i<cnt;i++)
	{
		rndNum = rand()%cnt;
		x = coord[rndNum].X;
		y = coord[rndNum].Y;
		while(isRandCoordRepeat(x,y,centerTmp,i+1))
		{
			rndNum = rand()%cnt;
			x = coord[rndNum].X;
			y = coord[rndNum].Y;
		}
		centerTmp[i].X = x;
		centerTmp[i].Y = y;
		if(i>k)
		{
			break;
		}
	}
	/*将中心点坐标赋值到全局变量*/
	for(i=0;i<k;i++)
	{
		g_center[i].X = centerTmp[i].X;
		g_center[i].Y = centerTmp[i].Y;
		g_center[i].tryCnt = 1;
		g_center[i].flag = 1;
		g_center[i].color = 0;
		packedDrawDot(centerTmp[i].X,centerTmp[i].Y,RGB(255,0,0),g_hdc);
	}
}

2.3.对点集进行分组

下面的代码中，夏树封装了一些使用GDI划线、画点以及输出文字的函数(方便自己用吧。不过如果是作业的VC下也有EasyX封装的绘图可以用，感兴趣的话可以自己了解一下?)

HDC packedGetDC();
void packedDrawDot(int x,int y,int color,HDC hdc);
void packedDrawLine(int xS,int yS, int xE, int yE, int color,HDC hdc);
void packedPrintText(int x,int y,char str[],int len,int color,HDC hdc);

然后计算所有点到每个中心点的距离，将点归到距离最近的中心点的分组中(因为课设题目中最多只分成10组, 下面输出组数的时候偷懒了一下)。

/*分组中心点(第n次分组)*/
void groupCenterDot(COORD coord[], int cnt, struct CENTER center[], int k)
{
	char cnum[5]={0};
	int i,j,minI,len;
	double distance,minDistance;
	/*设置分组颜色*/
	srand((unsigned)time(0));
	for(i=0;i<k;i++)
	{
		if(!center[i].color){
			center[i].color = RGB(rand()%255+1,rand()%255+1,rand()%255+1);
		}
	}
	/*计算到中心点最短距离并分组*/
	for(i=0;i<cnt;i++)
	{
		minDistance=-1;
		minI=-1;
		for(j=0;j<k;j++)
		{
			distance = (int)sqrt((coord[i].X-center[j].X)*(coord[i].X-center[j].X)+(coord[i].Y-center[j].Y)*(coord[i].Y-center[j].Y));
			if(minDistance<0)
			{
				minDistance = distance;
				minI = j;
				continue;
			}
			if(distance<minDistance)
			{
				minDistance = distance;
				minI = j;
			}
		}

		g_group[i] = minI;
	}
	/*绘制所有点编号*/
	for(i=0;i<cnt;i++)
	{
		j=g_group[i]+1;
		len=0;
		if(j<10)
		{
			cnum[0]=j+'0';
			len=1;
		}
		else if(j==10)
		{
			cnum[0]='1';
			cnum[1]='0';
			len=2;
		}
		packedDrawLine(coord[i].X,coord[i].Y,center[g_group[i]].X,center[g_group[i]].Y,center[g_group[i]].color,g_hdc);
		packedPrintText(coord[i].X,coord[i].Y,cnum,len,RGB(255,255,255),g_hdc);
	}
}

2.4.微调分组中心点

计算各个分组中所有点x的平均值和y的平均值，以这个平均值作为新的中心点，在微调中心点后重复2.3的分组操作。

那么，怎么判断是否应该结束分组了呢?
夏树这边对单个点的结束分组做了两种判断: (1)当计算出的x的平均值与上次中心点的x相差在1以内(y同理) (2)否则, 单个中心点的分组次数+1, 当分组次数大于等于设置的MAXTRY(1000次)时结束该点的分组
当所有点的分组都结束时，结束分组，并返回2.3绘制分组结果

/*更新中心点*/
void trimCenterDot(COORD coord[], int cnt, struct CENTER center[], int k)
{
	int i,j,groupNum,tag=0;
	double avgX,avgY;
	for(i=0;i<k;i++)
	{
		if(!center[i].flag) continue;
		avgX = 0;
		avgY = 0;
		groupNum=0;
		for(j=0;j<cnt;j++)
		{
			if(g_group[j]!=i) continue;
			avgX+=coord[j].X;
			avgY+=coord[j].Y;
			groupNum++;
		}
		avgX/=groupNum;
		avgY/=groupNum;
		//误差及微调阈值
		if((int)avgX-center[i].X<=DIFF && (int)avgY-center[i].Y<=DIFF)
		{
			center[i].flag = 0;
			continue;
		}
		else
		{
			if(center[i].tryCnt>=MAXTRY)
			{
				center[i].flag = 0;
				continue;
			}
			center[i].X = (int)avgX;
			center[i].Y = (int)avgY;
			center[i].tryCnt++;
		}
	}
	//遍历所有中心点是否可以微调
	for(i=0;i<k;i++)
	{
		if(center[i].flag)
		{
			tag=1;
			return;
		}
	}
	if(!tag)
	{
		g_tag = 0;
	}
}

3.一些参考

4.结束语

大概思路就是这些啦, 虽然代码还是有点乱, 没有做到太好的规范, 夏树之后也会继续努力der

本文最终实现效果源代码 Github: https://github.com/natukicc/kmeans-best-grouping

(完)

发布者

Natuki

I, Natuki

《夏树的C语言篇 – 简易Kmeans类聚算法实现对点集的分组》上有1条评论

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注